[Stochastic Process] 1. 확률과정(Stochastic Process)

이번 글에서는 확률과정의 수학적 정의와 함께 간단한 예시를 통해 확률과정이 무엇인지에 대해 알아보겠습니다.

---

먼저 예시를 보겠습니다. 

A회사에서는 인체에 해가 적고 자연상태에서 쉽게 분해되는 새로운 세제를 개발하였습니다. 그러나 이 제품은 기존제품에 비해 제조단가가 1.5배 이상 되어 과연 소비자들이 이를 선택할지 의문인 상황입니다. 따라서 경영자는 먼저 시제품을 내어놓고 이에 대한 소비자들의 반응을 알아볼 것 입니다. 또한 소비자들의 반응에 따라 생산량을 조절하여 적정 재고량을 유지하려 할 것 입니다. 그러자면 생산설비를 늘려야 할 것인지 줄여야 할 것 인지를 미리 판단하여야 하며 이를 위해서는 일정시간 경과 후에 신제품을 구입하고자 하는 소비자 수를 예측하여야 할 것 입니다. 

위의 예시와 같이 시간에 따라 상태가 확률적으로 변할 때, 그것을 수학적으로 모델링 하기 위한 도구가 확률과정입니다.

---

확률과정의 수학적 정의는 다음과 같습니다.

임의의 $t \in T$에 대하여 $X_t$가 확률공간상에 정의된 확률변수 일 때 확률변수들의 집합 $\{ X_t|t \in T \}$을 확률과정$Stochastic process or Random process$라고 합니다.

시점 $t$에서의 주식값 $X_t, \textrm{t in T}$를 $t$가 변함에 따라 추적해 나가면 하나의 확률과정이 형성됩니다. 여기서 $T$는 관찰시점들의 총집합을 나타내며 $T$를 지수집합$index set$ 또는 시간공간$time space$라고 부릅니다.

종종 $t$는 시간으로 해석되어지며 이때 실수 $X_t(w)=X(t, w)$는 시점$t$에서의 상태$state$ 또는 위치를 나타냅니다. 모든 $t \in T$에 대하여 $X_t$가 취할 수 있는 가능한 모든 값들의 집합 $S$를 상태공간$state space$라고 합니다.

또한 확률과정 $\{ X_t|t \in T \}$에서 각각의 $t$에 $X_t(w)$ 값을 대응시키는 관계를 표본 함수$Sample function$라 하고, $t$의 변화에 따른 $X_t$값의 그래프를 표본 경로$sample path$라고 합니다. $w \in \omega$가 고정되면 그때마다 하나의 표본경로를 그릴 수 있습니다.

삼성전자 주가 추이$20200716~20210716$

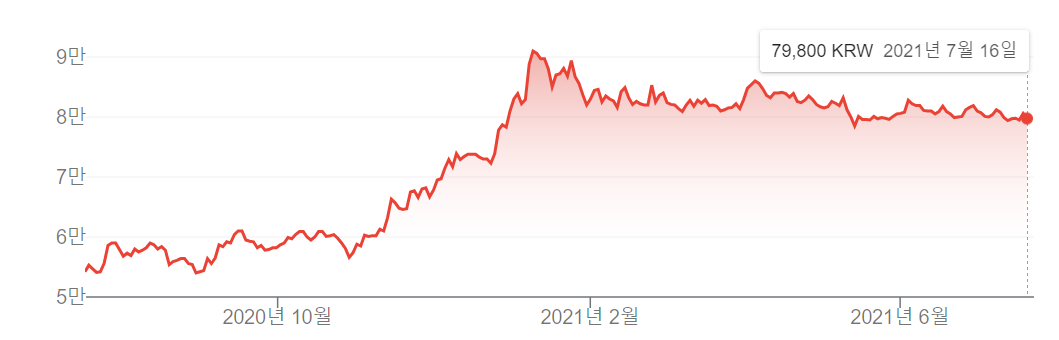
글을 쓰는 현재 시점인 2021년 7월 16일을 기준으로 1년간의 주가 추이는 다음과 같습니다. 삼성전자의 주가가 확률과정을 따른다고 가정하겠습니다.

위 그래프에서 지수집합$index set$은 2020년 7월 16일부터 2021년 7월 16일 입니다.

이 확률과정의 상태는 가격이며 2021년 7월 16일의 경우 79800원을 나타냅니다. 

---

확률 과정은 시간공간과 상태공간 그리고 종속관계에 따라 분류됩니다. 시간공간과 상태공간이 이산인지 연속인지에 따라 4가지 경우로 나눌 수 있습니다. 시간공간이 이산인 경우 이산시간확률과정, 연속인 경우 연속시간확률과정이라고 합니다.

$t$시점에서의 신제품 구입 소비자 수를 $X_t$라고 하면, $X_t$의 분포는 시간 $t$에 따라 변하게 되며 $X_t$ 사이에는 어떤 형태의 종속관계가 있는 것이 일반적입니다.  따라서 어떤 확률과정의 통계적 성질을 파악하기 위해 $X_1, \cdots,X_t$의 결합분포를 알아야 합니다. 그러나 확률과정 $\{ X_t|t \in T \}$이 특정한 구조를 갖고 있지 않다면 임의의 $n$개의 확률변수들의 결합분포를 모두 구한다는 것은 불가능합니다. 따라서 $X_t$ 사이에 적절한 종속관계를 가정한 다음 가정된 종속관계로부터 $X_1, \cdots,X_t$의 결합분포를 얻습니다.

$X_t$ 사이의 여러가지 종속관계에 따라 포아송과정, 마르코프과정, 재생과정, 마팅게일과정, 정상과정 등으로 분류할 수 있습니다. 그리고 확률과정이 특정한 분포를 따르도록 가정할 수 있습니다. 가우시안 분포를 따르도록 가정한 경우 Gaussian Process라고 하고, 디리클레 분포를 따르도록 가정한 경우 Dirichlet process라고 합니다.