2021. 7. 27. 22:48ㆍMachine Learning/Models
이번 글에서는 하나의 확률분포를 선형결합시켜 더 복잡한 형태를 만들 수 있는 혼합모델에 대해 알아보겠습니다.
이번 글에서는 여러 혼합모델 중 가장 널리 쓰이는 가우시안 혼합모델에 대해 알아 볼 것 이므로, 이전 글[Probability] 8. 정규분포와 중심극한정리(Normal distribution and Central limit theorem) 을 읽고 오시면 도움이 될 것 입니다.
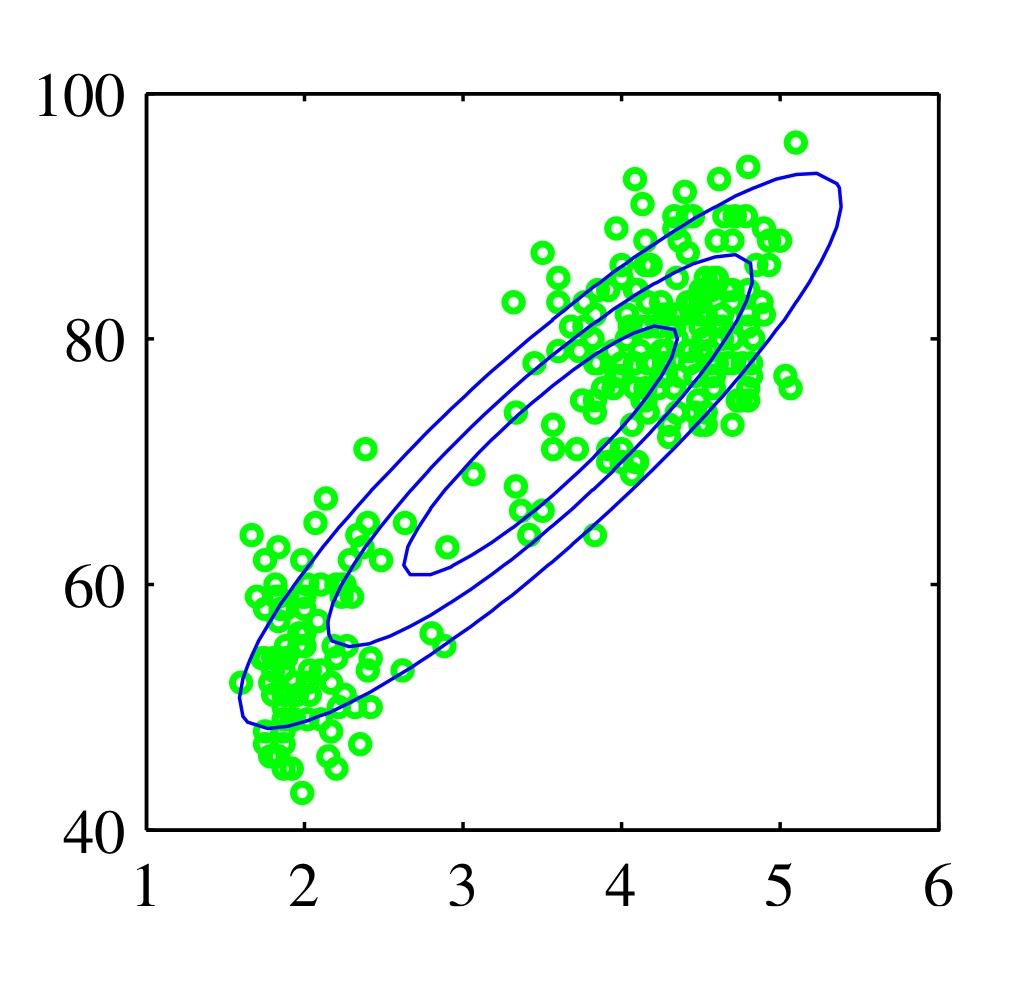
가우시안 분포는 수학적으로 좋은 특징이 많지만, 두 개로 나뉘어진 데이터를 정확하게 적합하지 못하는 문제가 있습니다. 만약 이 가우시안 분포를 선형결합(superposition)시킨다면, 더 복잡한 모양의 분포를 나타낼 수 있을 것 입니다.
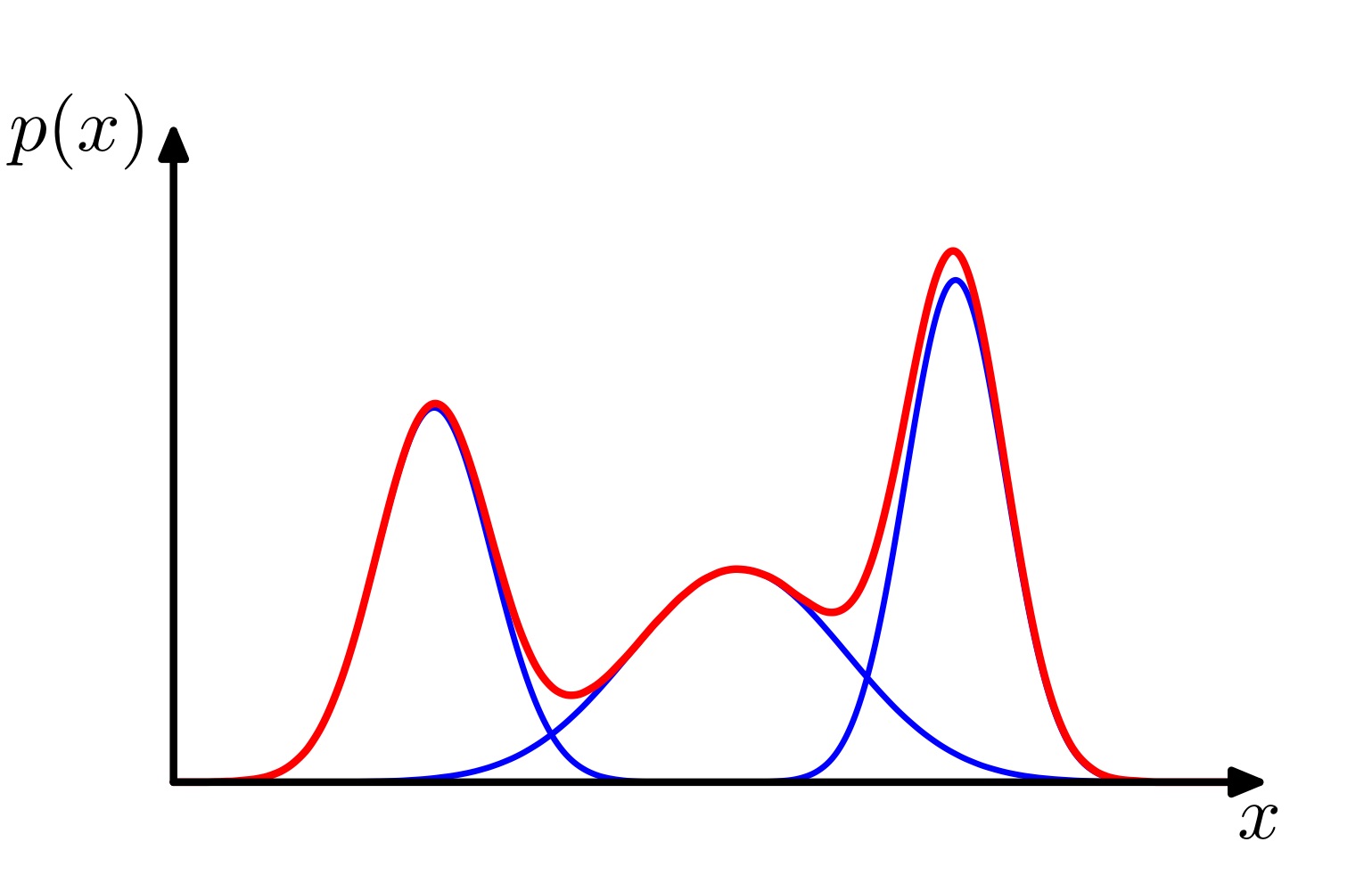
위 그림은 세 개의 가우시안분포(파란선)를 선형결합시킨 가우시안 혼합모델(Gaussian mixture model)입니다. 하나의 가우시안 분포를 사용하는 것 보다 훨씬 복잡한 경계를 만들어 낼 수 있습니다. 여러 개의 가우시안 분포를 선형결합하여 만든 가우시안 혼합모델은 다음과 같습니다.
$p(\textbf{x})=\displaystyle \sum^{K}_{k=1}{\pi_k N(\textbf{x}|\mu_k,~\Sigma_k)}$
여기서 $\pi_k$는 mixing coefficients로 각각의 가우시안 분포의 섞일 비중을 결정합니다.
단일 가우시안 분포를 적합 시킬 때, 로그 우도를 쓰게 되는데, 가우시안 혼합 모델에서의 로그 우도는 다음과 같습니다.
$\textrm{ln}p(\textbf{X}|\pi,~\mu,~\Sigma)=\displaystyle \sum^{N}_{n=1} ln \left \{ \displaystyle \sum^{K}_{k=1}{\pi_k N(\textbf{x}_n|\mu_k,~\Sigma_k)} \right \} $
가우시안 혼합모델의 로그 우도는 로그의 괄호 안에 식이 있기 때문에, 이 로그 우도를 닫힌 형식(closed-form)으로 미분하는 것이 어렵습니다. 따라서, 가우시안 혼합모델은 최대우도추정법(MLE)으로 적합시킬 수 없고, 다른 방법으로 적합시켜야 합니다.
'Machine Learning > Models' 카테고리의 다른 글
| [models] 주성분 분석(Principal Component Analysis) (0) | 2021.08.16 |
|---|---|
| [models] 가우시안 혼합모델의 확장(Extention of Gaussian Mixture) (0) | 2021.07.28 |
| [models] 회귀분석(Regression Analysis)과 최소자승법(Least Square Method) (0) | 2021.07.12 |