2021. 7. 11. 18:24ㆍMachine Learning/General
이전 글([Machine Learning] - 2-1. 편향-분산 절충 관계 증명(Bias-Variance Trade-off Proof))에서 모델을 학습하는 과정에서 사용되는 식을 예측모델의 편향과 분산으로 나눌 수 있음을 증명하였습니다.
이번 글에서는 예측모델 관점에서의 과대 적합과 과소 적합에 대해 알아보겠습니다.
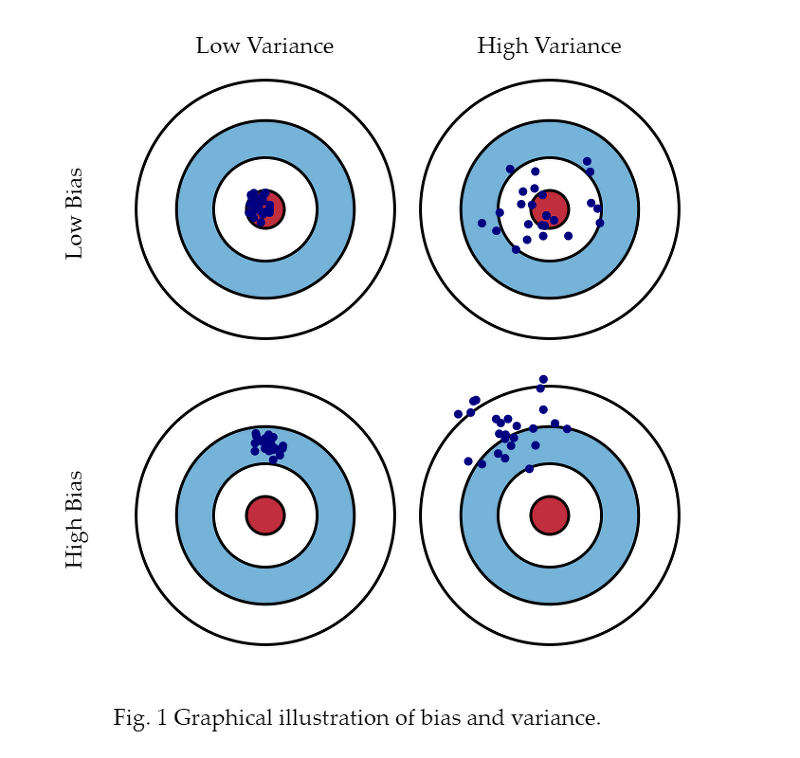
우리가 예측모델을 학습시킬 때, 왼쪽 상단의 모습처럼 분산도 낮고 편향도 낮은 모델을 학습시키는 것이 가장 이상적인 그림입니다. 하지만, 예측모델의 편향과 분산의 합은 정해져 있기 때문에, 둘 간의 절충 관계가 생기게 됩니다.
오른쪽 상단과 같이 훈련 데이터에 대해 편향은 낮지만, 분산이 높은 경우를 가리켜 "모델이 훈련 데이터에 과대 적합되었다"라고 말합니다. 즉, 훈련 데이터의 정답은 잘 맞힐 수 있지만, 새로운 데이터의 정답은 잘 맞힐 수 없음을 의미합니다.
왼쪽 하단과 같이 훈련 데이터에 대해 편향은 높지만, 분산이 낮은 경우를 가르쳐 "모델이 훈련 데이터에 과소 적합되었다"라고 말합니다. 즉, 훈련 데이터의 정답은 잘 맞히지 못하지만, 새로운 데이터에 대해서도 강건하게 예측 결과를 생성하는 것을 의미합니다.
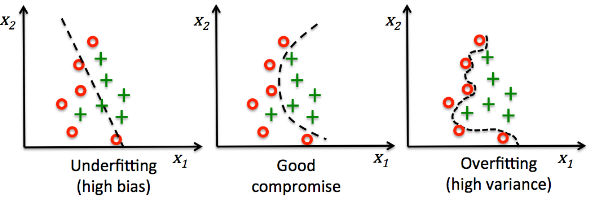
그렇다면, 어떤 경우에 과대 적합과 과소 적합이 일어나게 될까요?
왼쪽 그림에서 볼 수 있듯이, 모델이 결정 경계를 지나치게 선형으로 학습했을 때, 과소 적합이 일어나는 것을 알 수 있습니다. 따라서 모델이 결정 경계를 조금 더 비선형으로 학습할 수 있다면, 과소 적합 문제를 해결할 수 있을 것입니다.
오른쪽 그림에서 볼 수 있듯이, 모델이 결정 경계를 지나치게 비선형으로 학습했을 때, 즉 모델이 너무 복잡하고 모수의 수가 너무 많을 때, 과대 적합이 일어나는 것을 알 수 있습니다. 따라서 모델이 결정 경계를 조금 더 선형적으로 학습하여 강건한(Robust) 모델을 만들 수 있다면 과대 적합 문제를 해결할 수 있을 것입니다.